Hằng đẳng thức là một công cụ quan trọng trong toán học, đặc biệt là trong đại số. Chúng không chỉ giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả mà còn cung cấp cái nhìn sâu sắc về mối quan hệ giữa các biểu thức đại số. Trong bài viết này, chúng ta sẽ khám phá 7 hằng đẳng thức đáng nhớ, những công thức mà mọi học sinh, sinh viên và người yêu toán học nên nắm vững. Chúng ta sẽ tìm hiểu về định nghĩa, cách áp dụng, và thực hành thông qua các ví dụ cụ thể và bài tập. Hãy cùng bắt đầu cuộc hành trình khám phá thế giới của hằng đẳng thức!
Khái niệm và công thức về 7 hằng đẳng thức
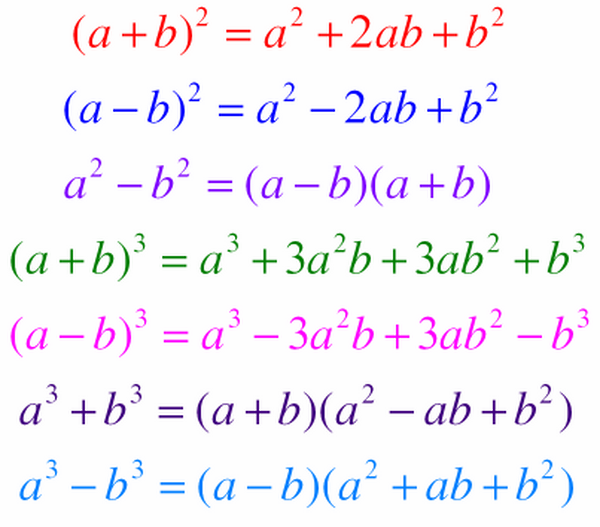
Hằng đẳng thức là một phương trình hoặc biểu thức đúng với mọi giá trị của biến số trong miền xác định của nó. Trong phần này, chúng ta sẽ tìm hiểu về 7 hằng đẳng thức quan trọng và phổ biến nhất trong đại số.
1. Bình phương của tổng và hiệu
Hai hằng đẳng thức đầu tiên chúng ta sẽ xem xét là bình phương của tổng và bình phương của hiệu. Đây là những công thức cơ bản nhưng vô cùng hữu ích trong nhiều tình huống.
- Bình phương của tổng: (a + b)² = a² + 2ab + b²
- Bình phương của hiệu: (a – b)² = a² – 2ab + b²
Những hằng đẳng thức này cho chúng ta thấy rằng bình phương của một tổng (hoặc hiệu) không chỉ đơn giản là tổng (hoặc hiệu) của các bình phương. Thành phần 2ab (hoặc -2ab) đóng vai trò quan trọng và thường được gọi là hạng chéo 2. Hiệu bình phương
Hằng đẳng thức tiếp theo là hiệu bình phương, một công thức rất hữu ích trong việc phân tích thừa số.
- Hiệu bình phương: a² – b² = (a + b)(a – b)
Công thức này cho phép chúng ta chuyển đổi hiệu của hai bình phương thành tích của tổng và hiệu của hai số. Đây là một công cụ mạnh mẽ trong việc đơn giản hóa biểu thức đại số và giải phương trình.
2. Lập phương của tổng và hiệu
Hai hằng đẳng thức tiếp theo liên quan đến lập phương của tổng và hiệu. Chúng phức tạp hơn so với bình phương, nhưng cũng rất quan trọng trong nhiều bài toán đại số.
- Lập phương của tổng: (a + b)³ = a³ + 3a²b + 3ab² + b³
- Lập phương của hiệu: (a – b)³ = a³ – 3a²b + 3ab² – b³
Những công thức này cho thấy sự phức tạp tăng lên khi chúng ta chuyển từ bình phương sang lập phương. Các số hạng trung gian (3a²b và 3ab²) đóng vai trò quan trọng và không thể bỏ qua.
3. Tổng và hiệu của lập phương
Hai hằng đẳng thức cuối cùng trong danh sách này liên quan đến tổng và hiệu của các lập phương.
- Tổng của lập phương: a³ + b³ = (a + b)(a² – ab + b²)
- Hiệu của lập phương: a³ – b³ = (a – b)(a² + ab + b²)
Những công thức này cho phép chúng ta phân tích thừa số tổng hoặc hiệu của hai lập phương. Chúng đặc biệt hữu ích trong việc giải các phương trình bậc ba và các bài toán liên quan đến lập phương.
7 hằng đẳng thức này tạo thành một bộ công cụ mạnh mẽ trong đại số. Chúng không chỉ giúp chúng ta tính toán nhanh chóng và chính xác mà còn cung cấp cái nhìn sâu sắc về cấu trúc của các biểu thức đại số. Trong các phần tiếp theo, chúng ta sẽ xem xét cách áp dụng những hằng đẳng thức này trong các ví dụ cụ thể và bài tập.
Các ví dụ về 7 hằng đẳng thức đáng nhớ

Để hiểu rõ hơn về cách áp dụng 7 hằng đẳng thức đã đề cập, chúng ta sẽ xem xét một số ví dụ cụ thể. Mỗi ví dụ sẽ minh họa cách sử dụng một hoặc nhiều hằng đẳng thức để giải quyết các vấn đề đại số.
Ví dụ về bình phương của tổng và hiệu
Hằng đẳng thức bình phương của tổng và hiệu thường được sử dụng để mở rộng hoặc rút gọn các biểu thức đại số.
- Tính giá trị của (3x + 2)² khi x = 5
Sử dụng hằng đẳng thức (a + b)² = a² + 2ab + b², ta có: (3x + 2)² = (3x)² + 2(3x)(2) + 2²
= 9x² + 12x + 4Khi x = 5: (3(5) + 2)² = 9(5)² + 12(5) + 4
= 9(25) + 60 + 4 = 225 + 60 + 4 = 289
- Rút gọn biểu thức: 4x² – 12x + 9
Nhận thấy đây có thể là dạng của (a – b)² = a² – 2ab + b², ta có thể viết lại: 4x² – 12x + 9 = (2x)² – 2(2x)(3) + 3²
= (2x - 3)²
Ví dụ về hiệu bình phương
Hằng đẳng thức hiệu bình phương thường được sử dụng trong phân tích thừa số và đơn giản hóa biểu thức.
- Phân tích thừa số: x² – 16
Sử dụng hằng đẳng thức a² – b² = (a + b)(a – b), ta có: x² – 16 = x² – 4²
= (x + 4)(x - 4)
- Tính giá trị của (101)² – (99)²
Thay vì tính riêng từng bình phương rồi trừ, ta có thể sử dụng hằng đẳng thức: (101)² – (99)² = (101 + 99)(101 – 99)
= 200 × 2 = 400
Ví dụ về lập phương của tổng và hiệu
Hằng đẳng thức lập phương của tổng và hiệu thường xuất hiện trong các bài toán liên quan đến khối lập phương và trong một số phương trình bậc ba.
- Tính thể tích của một khối lập phương có cạnh (x + 2) cm
Thể tích của khối lập phương là lập phương của cạnh: V = (x + 2)³
= x³ + 3x²(2) + 3x(2)² + 2³ = x³ + 6x² + 12x + 8
- Rút gọn biểu thức: x³ – 27y³ Sử dụng hằng đẳng thức a³ – b³ = (a – b)(a² + ab + b²), ta có: x³ – 27y³ = (x – 3y)(x² + 3xy + 9y²)
Những ví dụ này cho thấy cách hằng đẳng thức lập phương có thể được áp dụng trong các tình huống thực tế và trong việc đơn giản hóa biểu thức đại số phức tạp.
Ví dụ tổng hợp
Để minh họa cách các hằng đẳng thức có thể được sử dụng kết hợp, hãy xem xét ví dụ sau:
Rút gọn biểu thức: (x + 1)² – (x – 1)²
Bước 1: Sử dụng hằng đẳng thức bình phương của tổng và hiệu (x + 1)² = x² + 2x + 1 (x – 1)² = x² – 2x + 1
Bước 2: Thay vào biểu thức ban đầu (x + 1)² – (x – 1)² = (x² + 2x + 1) – (x² – 2x + 1)
Bước 3: Rút gọn = x² + 2x + 1 – x² + 2x – 1 = 4x
Ví dụ này cho thấy cách kết hợp nhiều hằng đẳng thức có thể giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả.
Tóm lại, thông qua các ví dụ này, chúng ta có thể thấy rằng 7 hằng đẳng thức đáng nhớ không chỉ là những công thức cần ghi nhớ, mà còn là những công cụ mạnh mẽ giúp chúng ta giải quyết nhiều loại bài toán đại số khác nhau. Việc thành thạo sử dụng chúng sẽ giúp chúng ta tiết kiệm thời gian và nâng cao hiệu quả trong việc giải toán.
Bài tập về bảy hằng đẳng thức đáng nhớ

Để củng cố kiến thức và kỹ năng áp dụng 7 hằng đẳng thức đáng nhớ, chúng ta sẽ thực hành thông qua một số bài tập. Mỗi bài tập sẽ tập trung vào một hoặc nhiều hằng đẳng thức, giúp chúng ta hiểu sâu hơn về cách sử dụng chúng trong các tình huống khác nhau.
Bài tập về bình phương của tổng và hiệu
- Tính giá trị của biểu thức sau khi x = 3 và y = 2: A = (x + y)² – (x – y)²
- Rút gọn biểu thức sau: B = 9x² + 24xy + 16y²
- Tìm giá trị của a để biểu thức sau là một hằng đẳng thức: C = x² + 2ax + 4 – (x – 2)²
Bài tập về hiệu bình phương
- Phân tích thừa số các biểu thức sau:
- 25x² – 49y²
- 4a² – b²
- Tính giá trị của biểu thức sau mà không cần tính từng số hạng: D = 101² – 99²
Bài tập về lập phương của tổng và hiệu
- Khai triển các biểu thức sau:
- (2x + 1)³
- (3y – 2)³
- Một khối lập phương có cạnh (x + 2) cm. Tính thể tích của khối lập phương này theo x.
Bài tập về tổng và hiệu của lập phương
- Phân tích thừa số các biểu thức sau:
- x³ + 8
- 27a³ – 125b³
- Giải phương trình: x³ + 27 = 0
Bài tập tổng hợp
- Rút gọn biểu thức sau:
E = (x + 2)³ - (x - 2)³
- Tính giá trị của biểu thức sau khi a = 5:
F = (a + 1)² - (a - 1)² + (a + 2)³ - (a - 2)³
- Chứng minh rằng với mọi số thực x, biểu thức sau luôn bằng 1:
G = (x + 1/x)² - (x - 1/x)² - 4
Những bài tập này đòi hỏi việc áp dụng linh hoạt các hằng đẳng thức đã học.
Cách giải bài tập về 7 hằng đẳng thức
Để giải các bài tập liên quan đến 7 hằng đẳng thức đáng nhớ trong đại số, chúng ta cần áp dụng kiến thức về các công thức cơ bản và kỹ năng phân tích biểu thức. Dưới đây là cách giải một số bài tập ví dụ để minh họa:
Bài tập ví dụ 1: Tính giá trị của biểu thức A = (x + y)² – (x – y)² khi x = 3 và y = 2
Đầu tiên, chúng ta sẽ thay các giá trị x và y vào biểu thức A: A = (3 + 2)² – (3 – 2)² A = 5² – 1² A = 25 – 1 A = 24
Vậy giá trị của biểu thức A khi x = 3 và y = 2 là 24.
Bài tập ví dụ 2: Rút gọn biểu thức B = 9x² + 24xy + 16y²
Để rút gọn biểu thức B, chúng ta sẽ sử dụng hằng đẳng thức lập phương của tổng và hiệu: B = (3x + 4y)² B = 9x² + 12xy + 12xy + 16y² B = 9x² + 24xy + 16y²
Vậy biểu thức B đã được rút gọn thành dạng (3x + 4y)².
Bài tập ví dụ 3: Tìm giá trị của a để biểu thức C = x² + 2ax + 4 – (x – 2)² là một hằng đẳng thức
Để biểu thức C là một hằng đẳng thức, ta cần rút gọn biểu thức (x – 2)² và so sánh với biểu thức ban đầu: C = x² + 2ax + 4 – (x – 2)² C = x² + 2ax + 4 – (x² – 4x + 4) C = x² + 2ax + 4 – x² + 4x – 4 C = 2ax + 4x
So sánh với biểu thức ban đầu, ta có: 2ax + 4x = x² + 2ax + 4 4x = x² + 4 x² – 4x + 4 = 0 (x – 2)² = 0 x = 2
Vậy giá trị của a để biểu thức C là một hằng đẳng thức là a = 2 khi x = 2.
Qua các ví dụ trên, chúng ta có thể thấy cách áp dụng các hằng đẳng thức để giải các bài tập đại số một cách linh hoạt và chính xác. Việc hiểu rõ về các công thức và biết cách áp dụng chúng sẽ giúp chúng ta giải quyết các bài toán một cách dễ dàng và nhanh chóng.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về 7 hằng đẳng thức đáng nhớ trong đại số, bao gồm khái niệm, công thức cũng như các ví dụ và bài tập minh họa. Qua việc áp dụng các hằng đẳng thức này, chúng ta có thể giải quyết nhiều loại bài toán đại số khác nhau một cách hiệu quả. Việc rèn luyện kỹ năng sử dụng các hằng đẳng thức này sẽ giúp chúng ta trở thành những người giỏi toán học và nâng cao khả năng giải quyết vấn đề. Hy vọng rằng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và kiến thức cần thiết về chủ đề này. Hãy thực hành và áp dụng những kiến thức này vào thực tế để phát triển khả năng toán học của mình. Chúc các bạn thành công!
